Вначале был свет…
Самое смешное в высоких технологиях — это то, что им уже тысячи лет! Например, счисление было изобретено независимо Ньютоном и Лейбницом более 300 лет назад. То, что когда-то считалось магией, сейчас хорошо изучено. И, конечно, все мы знаем, что геометрию изобрёл Евклид пару тысяч лет назад. Фишка в том, что зачастую проходят годы прежде, чем что-то становится «популярным». Нейронные сети — превосходный пример. Все мы слышали о нейронных сетях и о том, что они обещают, но почему-то не видим обычных программ, основанных на них. Причиной этого является то, что истинной природой нейронных сетей является чрезвычайно сложная математика, и необходимо понимать и доказывать сложные теоремы, которые её охватывают, и, возможно, необходидмо знание теории вероятности и комбинаторного анализа, не говоря уже о физиологии и неврологии.
Стимул к созданию любой технологии для человека или людей — это создание Программы-Убийцы с её помощью. Все мы сейчас знаем, как рабоает DOOM, т.е. используя деревья BSP. Однако Джон Кармак в своё время не изобрёл их, он прочитал о них в статье, написанной в 1960 году. Эта статья описывала теорию BSP-технологии. Джон сделал следующий шаг, поняв, как могут быть использованы BSP-деревья, и родился DOOM. Я подозреваю, что нейронные сети ожидает такое же перерождение в ближайшие несколько лет. Компьютеры достаточно быстры для их имитации, VLSI-дизайнеры создают их прямо в кремнии, и есть сотни опубликованных книг по этой тематке. А поскольку нейронные сети — наиболее математическая сущность из всего нам известного, они не привязаны к какому-либо физическому представлению и мы можем создать их при помощи программного обеспечения или создать реальные кремниевые модели. Главное, что суть нейронной сети — абстрактная модель.
Во многих отношениях пределы цифровых вычислительных машин уже были реализованы. Конечно, мы будем совершенствовать их и делать ещё быстрее, меньше и дешевле, но цифровые компьютеры всегда смогут воспринимать только цифровую информацию, поскольку основаны они на бинарной вычислительной модели. Нейронные сети, однако, основаны на разных моделях вычислений. Они основаны на высокоуровневой распределённой, вероятностной модели, которая не обязана искать решение проблемы так, как это делает компьютерная программа; она моделирует сеть ячеек, которые могут найти, установить или кореллировать возможные пути решения проблемы более «биологическим» путём, решая проблему маленькими кусочками и складывая результаты вместе. Эта статья — обзор технологии нейронных сетей, где они будут разобраны настолько подробно, насколько это возможно на нескольких страницах.
Биологические аналоги
Нейронные сети были вдохновлены нашим собственным мозгом. Буквально — чей-то мозг в чьей-то голове как-то сказал: «меня интересует, как же я работаю?», а затем приступил к созданию простой модели самого себя. Странно, да? Модель стандартной нейронной ноды, основанная на упрощенной модели человеческого нейрона, изобретена более пятидесяти лет назад. Взгляните на рисунок 1.0. Как вы можете видеть, есть три основных части нейрона, это:
- Дентрит(ы) (Dendrite)……………….Ответственны за сбор поступающих сигналов
- Сома (Soma)…………………………..Ответственны за основную обработку и суммирование сигналов
- Аксон (Axon)………………………….Отвечает за передачу сигналов другим дендритам.
Средний человеческий мозг содержит около 100 млрд. или 10 в 11-й степени нейронов, и каждый из них имеет до 10000 соединений через дендриты. Сигналы передаются с помощью электрохимических процессов на основе натрия, калия и ионов. Сигналы передаются, накапливая разницу потенциалов, вызванную этими ионами, но химия тут значения не имеет, и сигналы можно рассматривать как простые электрические импульсы, путешествующие с аксона на дендрит. Присоединение одного дентрита к чужому аксону называется синапс, и это основные точки передачи импульсов.
Так как же работает нейрон? На этот вопрос нет простого ответа, но для наших целей будет достаточно следующего обьяснения. Дендриды собирают сигналы, полученные от других нейронов, затем сомы выполняют суммирование и вычисление сигналов и данных, и наконец на основе результата обработки могут «сказать» аксонам передать сигнал дальше. Передача далее зависит от ряда факторов, но мы можем смоделировать это поведение как передаточную функцию, которая принимает входные данные, обрабатывает их и готовит выходные данные, если выполняются свойства передаточной функции. Кроме того, в реальных нейронах вывод данных нелинеен, то есть сигналы — не цифровые, а аналоговые. Фактически нейроны непрерывно получают и передают сигналы и реальная их модель зависит от частоты и должна быть проанализирована в S-домене (домене частоты). Реальная передаточная функция простого биологического нейрона по сути нами смоделирована.
Теперь у нас есть некоторое представление о том, что такое нейроны и что мы собственно пытаемся смоделировать. Давайте отвлечемся на минуту и поговорим о том, как мы можем использовать нейронные сети в видеоиграх.
Игры
Нейронные сети, похоже, могут стать ответом на все наши потребности. Если бы мы могли передавать символы и слова в маленькие игровые мозги, представьте, как круто это было бы. Модель нейронных сетей даёт нам грубую структуру нейронов, но не даёт высокого уровня функциональности разума и дедукции, по крайней мере в классическом смысле этого слова. Придётся немного подумать, чтобы придумать способы применения технологии нейронных сетей в игровом ИИ, но как только вы это сделаете, вы сможете использовать их в связке с детерминированными алгоритмами, нечеткой логикой и генетическими алгоритмами для создания весьма надежной и продвинутой модели мышления ИИ для ваших игр. Вне сомнения результат будет лучше всего того, чего вы способны достичь сотнями блоков if-else или скриптами сценариев. Нейронные сети могут быть использованы для таких вещей, как:
Сканирование и распознавание окружения — нейронная сеть может получать информацию в виде зрения или слуха. Затем эта информация может быть использована для формирования ответа или реакции, или для обучения сети. Эти ответы могут быть выведены в режиме реального времени и обновлены с целью оптимизации ответов.
Память — нейронная сеть может быть использована как форма памяти игровых персонажей. Нейронные сети могут обучаться на собственном опыте и пополнять набор ответов и реакций.
Поведенческий контроль — выходные данные нейронной сети могут быть использованы для контроля дейтвий игрового персонажа. Входными могут быть различные переменные движка игры. Тогда сеть сможет контролировать поведение игрового персонажа.
Маппинг ответов — нейронные сети действительно хорошо работают с «ассоциациями», что по сути — привязка одного пространства к другому. Ассоциация поставляется в двух вариантах: автоассоциация, связывающия ввод с самим собой, и гетероассоциация, связывающая ввод с чем-то еще. Связывание ответов использует нейронные сети как бэк-енд или вывод для создания ещё одного слоя косвенного управления поведением объекта. Как правило, мы могли бы иметь ряд контрольных переменных, но у нас есть только четкие ответы на ряд определённых комбинаций, которым мы можем обучить сеть. Однако используя нейронную сеть на выходе мы можем получить другие ответы, которые находятся примерно в той же области, что и наши четко предопределенные.
Приведённые примеры могу показаться несколько нечеткими, так и есть. Дело в том, что нейронные сети — это инструмент, который мы можем использовать как нам угодно. Ключевым тут является то, что их использование делает задачу создания ИИ проще и позволит сделать поведение игровых персонажей более разумным.
Нейронные сети 101
В этом разделе мы рассмотрим основные термины и понятия, используемые при обсуждении нейронных сетей. Это не так просто, поскольку нейронные сети — действительно продукт нескольких разных дисциплин, и каждая из них тянет за собой свой специфический словарь. Увы, словарь, касающийся нейронных сетей — пересечение словарей всех этих дисциплин, поэтому рассмотреть всё мы просто не сможем. Кроме того, теория нейронных сетей изобилует оборудованием, которое является избыточным, а это значит, что многие люди заново изобретают колесо. Это оказало влияние на создание сразу ряда архитектур нейронных сетей, каждая из которых имеет своё название. Я постараюсь описывать общие термины и ситуации, чтобы не увязнуть в именовании. Ну и в этой статье мы рассмотрим некоторые сети, которые достаточно различаются, чтобы иметь различные названия. По мере чтения не слишком беспокойтесь, если не сможете сходу осознать все понятия и термины, просто читайте их, дальше мы постараемся охватить их снова в контексте статьи. Давайте начнём…
Теперь, когда мы увидели «биологическую» версию нейрона, давайте рассмотрим основы искуственного нейрона, чтобы задать базу нашим рассуждениям. Рис. 2.0 — графический стандарт «нейроноды» или искусственного нейрона. Как видите, он имеет несколько входов, помеченных как X1 — Xn и В. Эти входы имеют ассоциированный с ними вес W1-Wn, и присоединённый к ним b. Кроме того, есть суммарное соединение Y и один выход y. Выход y в нейроноде основан на передаточной ф-ия, или «активация», которая является функцией входа нейроноды в сеть. Входящие данные приходят от X-ов и от B, которые соединены с соседними узлами. Идея в том, что B — это «прошллое», «память». Основная операция нейроноды такова: входные данные от X умножаются на связанный с ними вес и суммируются. Выходные данные суммирования — входные данные для активации Ya. Активация затем подаётся на функцию активации fa(x) и финальный вывод — это y. Уравнение всего этого:
ур. 1.0
Ya = B*b + е Xi * wi
i =1AND
y = fa(Ya)
Различные формы fa(x) будут рассмотрены через минуту.
Прежде, чем продолжать, мы должны поговорить о вводных Xi, весах Wi, и соответствующих им областях. В большинстве случаев вводы содержат положительные и отрицательные числа во множестве (- ¥, + вводы = I). Однако много нейронных сетей используют простые двузначные значения (вроде true/false). Причина использования такой простой схемы то, что в конечном счете все сложные даные преобразуются в чистое бинарное представление. Кроме того, во многих случаях нам нужно решить такие компьютерные задачи, как распознавание голоса, которые как раз подходят для двузначных представлений. Тем не менее, это не высечено на камне. В любом случае значения, используемые в двухвалентной системе в первую очередь 0 и 1 в двоичной системе или -1 и 1 в биполярной системе. Обе системы аналогичны за исключением того, что биполярное представление оказывается математически удобнее, чем бинарное . Весы Wi на каждом входе как правило в промежутке между ( -Ґ , +Ґ ), и называются «возбуждающие» или «тормозящие» для положительных и отриицательных значений соответственно. Дополнительный вход B, который вседа вызывается с 1.0 и умножается на b, где b — его вес.
Продолжая наш анализ, после нахождения активации Ya для нейроноды, она применяется к функции активации и может быть вычислен результат. Существует ряд функций активации, имеющих различное применение. Основные функции активации Fa(x):
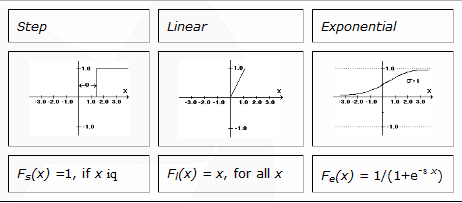
Пошаговая (step) функция используется в ряде нейронных сетей и моделей для достижения заданной критичности входнящего сигнала. Цель фактора q — моделирование критического уровня входящего сигнала, на который должен реагировать нейрон.
Линейная (linear) функция активации используется, когда мы хотим, чтобы вывод нейроноды как можно ближе следовал за входной активацией. Подобная функция может быть использована для создания линейных систем, таких, как движение с постоянной скоростью. Наконец, экспонентная функция — ключ к продвинутым нейронным сетям, единственный путь к созданию нейронных сетей, которые смогут давать нелинейные ответы и моделировать нелинейные процессы. Функция экспонентной активации является развилкой в развитии нейронных сетей, поскольку используя шаговые и лнейные функции мы никогда не сможем создать нейронную сеть, дающую нелинейный отклик. Однако мы не обязаны использовать именно эту функцию. Могут быть использованы и гиперболические, логарифмические и трансцендентальные функции в зависимости от желаемых свойств сети. Наконец, мы можем использовать все подобные функции, если захотим.
Как вы можете догадаться, один нейрон многого не сделает, поэтому необходимо создать группу нейронов и слой нейронод, как показано на рис. 3.0. Рисунок иллюстрирует небольшую однослойную нейронную сеть. Нейронная сеть на рис. 3.0 содержит ряд входных и выходных узлов. По принятому соглашению это однослойная нейронная сеть, т.к. входной слой не учитывается, если только он не единственный слой сети. В данном случае входной слой одновременно и выходной, поэтому сеть однослойная. Рис. 4.0 показывает двуслойную нейронную сеть. Обратите внимание, что входной слой по-прежнему не учитывается, а внутренний слой называют «скрытым». Выходной слой называют выводом ответного слоя. Теоретически не существует ограничений на количество слоёв в нейронной сети, однако может быть очень сложно описать отношения различных слоёв и приемлемые методы обучения. Лучший способ создания многослойной нейронной сети — сделать каждую сеть одно- или двуслойной, а затем соединить их как компоненты или функциональные блоки.
Хорошо, теперь давайте поговорим о «временном» или на тему времени. Мы все знаем, что наш мозг работает достаточно медленно по сравнению с цифровой вычислительной машиной. Фактически наш мозг производит один цикл в масштабе миллисекунд, в то время как время для цифрового компьютера исчисляется наносекундах и почти уже в суб-наносекундах. Это означает, что путь сигнала от нейрона к нейрону занимает некоторое время. Это также моделируется в искусственных нейронах в том смысле, что мы производим вычисления слой за слоем и выдам результаты последовательно. Это помогает смоделировать временной лаг, присутствующий в биологических системах, таких, как наш мозг.
Мы почти закончили предварительное обсуждение, давайте поговорим о некоторых высокоуровневых понятиях, а затем закончим на ещё парочке терминов. Вопрос, который вы должны задать: «в чём фишка нейронных сетей?» Это хороший вопрос, и окончательно на него ответить затруднительно. Расширенный вопрос — «Что вы хотите попытаться заставить делать нейронные сети?» В основном они отображают методику, которая помогает отразить одно пространство по отношению к другому. В сущности нейроны представляют собой тип памяти. И как и к любой памяти, мы можем применять для их описания некоторые соответствующие термины. нейроны имеют как STM (кратковременная память), так и LTM (долговременная память). STM — способность нейронной сети вспомнить что-то, что она узнала только что, а LTM — способность нейронной сети вспомнить что-то, что она узнала некоторое время назад в свете только что полученной информации. Это приводит нас к концепции пластичности или, другими словами, к концепции того, как нейронная сеть поведёт себя с информацией или при обучении. Может ли нейронная сеть изучать больше информации и продолжать верно «вспоминать» ранее изученную? Если да, то нейронные сети становятся неустойчивыми, поскольку будут в итоге содержать столько информации, что данные начнут бесконечно пересекаться и перекрывать друг друга. Это приводит нас к ещё одному требованию — стабильности. Итоговая суть — мы хотим, чтобы нейронная сеть обладала хорошей LTM, хорошей STM, была пластичной и проявляла стабильность. Конечно, некоторые нейронные сети не являются аналогом памяти, они направлены в основном на функциональное отображение, и к ним эти понятия не применяются, но вы поняли основную суть. Теперь, когда мы знаем о перечисленных понятиях, связанных с памятью, давайте завершим обзор на нескольких математических факторах, которые помогут оценить и понять эти свойства.
Одно из основных применений нейронных сетей — создание механизма воспоминаний, который сможет обрабатывать неполные либо нечеткие входные данные и возвращать результат. Результатом могут быть сами входные данные (ассоциация) или совершенно отличающийся от входных данных ответ (гетероассоциация). Также возможно наложение N-мерного пространства на M-мерное и нелинейная загрузка данных. Это означает, что нейронная сеть является своего рода гиперпространственным блоком памяти, поскольку может связать входной N-элемент с выходным M-элементом, где M может быть равно N, а может и не быть.
Что в сущности делают нейронные сети — разделяют N-мерное пространсово на регионы, которые однозначно сопоставляют входные данные с выходными или классифицируют входные данные в различные классы. Тогда при увеличении значений (векторов) входящего набора данных (назовём его S), логически следует, что нейронным сетям будет сложнее разделять информацию. И так как нейронные сети наполнены информацией, входные значения, которые должны быть «вспомнены», будут пересекаться, так как входящее пространство не может содержать все разделённые данные в бесконечном числе измерений. Это перекрытие означает, что некоторые входы не так сильны, как могли бы быть. Хотя в ряде случаев эта проблема не является проблемой, она вызывает озабоченность при моделировании нейронных сетей памяти; давайте для иллюстрации концепции предположим, что мы пытаемся связать N-набор входных векторов с некоторым множеством выходов. Выходное множество — не столь большая проблема для надлежащего функционирования, какой является выходной набор S.
Если входной сет S является строго двоичным, то мы рассматриваем последовательности вида 1101010 … 10110. Давайте скажем, что наши входные даные имеют только 3 бита каждый, поэтому все пространство входа состоит из векторов:
v0 = (0,0,0), v1 = (0,0,1), v2 = (0,1,0), v3 = (0,1,1), v4 = (1,0,0), v5 = (1,0,1), v6 = (1,1,0),
v7 = (1,1,1)
Для большей точности, базис для этого сета векторов:
v = (1,0,0) * b2 + (0,1,0) * b1 + (0,0,1) * b0, where bi can take on the values 0 or 1.
Например, если мы допустим, что B2=1, B1=0, и B0=1, то получим следующий вектор:
v = (1,0,0) * 1 + (0,1,0) * 0 + (0,0,1) * 1 = (1,0,0) + (0,0,0) + (0,0,1) = (1,0,1), который является Vs нашего возможного входного массива
Базис — это специальный суммированный вектор, описывающий массив векторов в пространстве. Так V описывает все векторы в нашем пространстве. В общем, не вдаваясь в долгие объяснения, чем более ортогональны векторы во входном массиве, тем лучше они будут распространяться в нейронной сети, и тем лучше могут быть вызваны. Ортогональность относится к независимости векторов, другими словами если два вектора ортогональны, то их скалярное произведение равно нулю, их проекция друг на друга равна нулю, и они не могут быть описаны относительно друг друга. В массиве v есть множество ортогональных векторов, но они приходят небольшими группами, например V0 Ортогонален всем векторам, поэтому мы можем всегда включать его. Но если мы включим V1 в массив S, то только векторы V2 и V4 будут поддерживать с ним ортогональность:
v0 = (0,0,0), v1 = (0,0,1), v2= (0,1,0), v4 = (1,0,0)
Почему? Потому что Vi — Vj для всех i,j от 0..3 равно нулю. Другими словами, скалярное произведение всех пар векторов в 0, поэтому они все должны быть ортогональны. Таким образом, этот массив очень хорош в качестве входного массива нейронной сети. Однако массив:
v6 = (1,1,0), v7 = (1,1,1)
потенциально плох, т.к. входы v6-v7 не-нулевые, в бинарной системе это 1. Следующий вопрос — мы можем измерить эту ортогональность? Ответ — Да. В двоичной системе векторов есть мера, называемая расстояние Хэмминга. Она используется для измерения N-мерного расстояния между двоичными векторами. Это просто число битов, которые различны у двух векторов. Например, векторы:
v0 = (0,0,0), v1 = (0,0,1)
имеют дистанцию Хэмминга 1 между собой, а
v2 = (0,1,0), v4 = (1,0,0)
имеют дистанцию хэмминга 2.
Мы можем использовать расстояние Хэмминга в качестве меры ортогональности в бинарных системах векторов. И это может помочь нам определить, имеют ли пересечения наши входные массивы данных. Определение ортогональности с общими входными векторами — сложнее, но принцип тот же. Пожалуй, достаточно концепций и терминологии, давайте перепрыгнем всё остальное и посмотрим на фактические нейронные сети, которые что-то делают и, возможно, в итоге прочтения этой статьи вы сможете использовать их для совершенствования ИИ вашей игры. Мы рассмотрим нейронные сети, используемые для выполнения логических функций, классификации входных данных и ассоциирования их с выходными.
Чистая логика
Первые искуственные нейронные сети были создана в 1943г. Маккалоком и Питтсом. Они состояли из некоторого числа нейроузлов и использовались в основном для вычисления простых логических функций, таких, как AND, OR, XOR и их комбинаций. Рис. 5.0. представляет собой основные нейроноды Маккалока и Питтса с двумя входами. Если вы инженер-электрик, то сразу увидите их близкое сходство с транзисторами. В любом случае, нейроноды Маккалока-Питтса не имеют соединений и простая функция активации Fmp(x) равна:
fmp(x) = 1, if xіq
0, if x < q
MP (McCulloch-Pitts)-нейронода функционирует путём суммирования произведения входов Xi и весов Wi и принимает как результат Ya для функции Fmp(x). Ранние исследования Маккалока-Питса были сосредоточены на создании сложных логических схем с моделями нейронод. Кроме того, одно из правил моделирования нейронод — то, что передача сигнала от нейрона к нейрону занимает один шаг времени. Это помогает быть ближе к модели природных нейронов. Давайте взглянем на некоторые примеры MP-нейронных сетей, реализующих базовый логический функционал. Логическая функция AND Имеет следующую таблице истинности:
Мы можем смоделировать это двумя входмыми MP-нейронными сетями с весами w1=1, w2=2, и q=2. Эта нейронная сеть показана на рис. 6.0а. Как видите, все входные комбинации работают верно. Например,если мы попытаемся задать вводные X1=0, Y1=1, то активация будет:
X1*w1 + X2*w2 = (1)*(1) + (0)*(1) = 1.0
Если мы применим 1.0 для функции активации Fmp(x), то результатом будет 0, что является верным ответом. Как другой пример, если мы попробуем задать вводные X1=1, X2=1, то активация будет:
X1*w1 + X2*w2 = (1)*(1) + (1)*(1) = 2.0
Если мы вводим 2.0 в функцию активации Fmp(x), результатом будет 1.0, что является верным. В других случаях работать будет аналогично. Функция ИЛИ аналогична, но чувствительность q изменяется на 1.0 вместо 2.0, как было в AND. Вы можете сами попробовать погонять данные через таблицы истинности, чтобы посмотреть на результаты.
Сеть XOR немного отличается, так как в действительности имеет 2 слоя, т.к. результаты предварительной обработки в дальнейшем обрабатываются в выходном нейроне. Это хороший пример того, почему нейронной сети необходим более чем один слой для решения определённых задач. XOR — это общая проблема нейронных сетей, которая обычно используется для теста производительности сети. В любом случае, XOR линейно неотделима в отдельный слой, она должна быть разбита на более мелкие этапы, результаты которых суммируются. Таблица истинности для XOR выглядит так:
XOR верна только когда вводы различны, это проблема, т.к. оба ввода относятся к одному выводу. XOR линейно неразделима, это показано на рис. 7.0. Как видите, не существует способа отделить верный ответ прямолинейно. Дело в том, что мы можем отделить верный ответ двумя линиями, и это как раз то, что делает второй слой. Первый слой предварительно обрабатывает данные или решает часть проблемы, а оставшийся слой завершает вычисление. Обращаясь к рис. 6.0 мы видим, что веса Wq=1, W2=-1, W3=1, W4=-1, W5=1, W6=1. Сеть работает следующим образом: слой вычисляется, если X1 и X2 являются противоположностями, результаты в случаях (0,1) или (1,0) являются пищей для слоя два, который их суммирует и передаёт дальше, если true. В сущности мы создали логическую функцию:
z = ((X1 AND NOT X2) OR (NOT X1 AND X2))
Если вы хотите поэкспериментировать с базовыми нейронодами Маккалока-Питтса, следующий листинг представляет собой полный стимулятор нейроноды с двумя входами.
/////////////////////////////////////////////////////// INCLUDES
/////////////////////////////////////////////////////
#include <conio.h>
#include <stdlib.h>
#include <malloc.h>
#include <memory.h>
#include <string.h>
#include <stdarg.h>
#include <stdio.h>
#include <math.h>
#include <io.h>
#include <fcntl.h>
// MAIN
/////////////////////////////////////////////////////
void main(void)
{
float threshold, // this is the theta term used to threshold the summation
w1,w2, // these hold the weights
x1,x2, // inputs to the neurode
y_in, // summed input activation
y_out; // final output of neurode
printf(«nMcCulloch-Pitts Single Neurode Simulator.n»);
printf(«nPlease Enter Threshold?»);
scanf(«%f»,&threshold);
printf(«nEnter value for weight w1?»);
scanf(«%f»,&w1);
printf(«nEnter value for weight w2?»);
scanf(«%f»,&w2);
printf(«nnBegining Simulation:»);
// enter main event loop
while(1)
{
printf(«nnSimulation Parms: threshold=%f, W=(%f,%f)n»,threshold,w1,w2);
// request inputs from user
printf(«nEnter input for X1?»);
scanf(«%f»,&x1);
printf(«nEnter input for X2?»);
scanf(«%f»,&x2);
// compute activation
y_in = x1*w1 + x2*w2;
// input result to activation function (simple binary step)
if(y_in >= threshold)
y_out = (float)1.0;
else
y_out = (float)0.0;
// print out result
printf(«nNeurode Output is %fn»,y_out);
// try again
printf(«nDo you wish to continue Y or N?»);
char ans[8];
scanf(«%s»,ans);
if(toupper(ans[0])!=‘Y’)
break;
} // end while
printf(«nnSimulation Complete.n»);
} // end main
На этом наше обсуждение базовых блоков МП-нейросети завершены, давайте двигаться к более комплексным нейронным сетям, таким как те, которые используются для классификации входных векторов.
Классификация и распознавание «изображений»
Наконец мы готовы рассмотреть реальные нейронные сети, которые нашли некоторое применение! Чтобы перейти к последующему обсуждению нейронных сетей Хебба и Хопфилда, проанализируем общую структуру нейронных сетей, которая проиллюстрирует ряд понятий, таких как линейная отделимость, биполярные представления, и аналогии, проходящие между нейронными сетями и воспоминаниями. Давайте для начала взглянем на рис. 8.0, которые представляет основную модель нейронной сети, которую мы собираемся использовать. Как видите, это одноузловая сеть с тремя входами, включающими смещение B, и одним выходом. Мы хотим увидеть, как использовать эту сеть для реализации логической операции AND, которую мы так просто реализовали в нейронодах Маккалока-Питтса.
Давайте начнем, используя биполярные представления, так что все 0 заменяются на -1. Таблица истинности для логического И при использовании биполярных входов и выходов показана ниже:
А вот функция активации fc(x), которую мы будем использовать:
fc(x) = 1, if x і q
-1, if x < q
Обратите внимание, что функция — это шаг к биполярному выводу. Прежде чем продолжить, позвольте мне посеять семена в вашем мозге: смешение и чувствительность в конечном итоге делают то же самое, они дают нам ещё одну степень свободы в наший нейронах, которая позволяет им создавать такие ответы, которые не могут быть достигнуты без неё. Скоро вы увидите это.
Единая нейронода на рис. 8.0 пытается выполнить для нас классификацию. Она собирается сказать нам, такого ли класса наш ввод или иного. Например, изображение ли это дерева, или нет. Или, в нашем случае (простое логическое AND), это +1 или -1 класс? Это основа большинства нейронных сетей, поэтому и говорил о линейной отделимости. Мы должны прийти к линейному разделению пространства, что соотнесет наши входы и выходы так, что появится твердое разделение пространства, их разделяющего. Таким образом нам нужно придумать правильные значения веса и смещения, которые сделают это для нас. Но как мы это сделаем? Просто используя метод проб и ошибок, или есть некая методология? Ответ таков: есть ряд методов обучения нейронной сети. Эти методы работают на различных математичесих примерах и могут быть доказаны, но в данный момент мы просто будем брать значения, которые работают, не рассматривая процесс их получения. Эти упражнения приведут нас к алгоритмам обучения и более сложных сетей, чем приведённые здесь.
Ладно, мы пытаемся найти веса Wi и смещение B, которые дадут правильный результат при различных вводимых данных с функцией активации Fc(x). Напишем активацию суммирования нашей нейроноды и посмотрим, можем ли мы создать любые соотношения между весом и вводными данными, которые могут нам помочь. Учитывая входы X1 и X2 с весами W1 и W2 вместе с B=1 и смещением b, мы получим следующую формулу:
X1*w1 + X2*w2 + B*b=q
Так как B всегда равно 1.0, формула упрощается до:
X1*w1 + X2*w2 + b=q
X2 = -X1*w1/w2 + (q -b)/w2 (solving in terms of X2)
Что это такое? Это линия! И если лева сторона больше или равна q, то есть (X1*W1+X2*W2+b), то нейронода ответит 1, иначе выдаст результат -1. Т.е. линия — это границы решения. Рис. 9.0 иллюстрирует это. На графике вы можете увидеть, что наклон линии — это -w1/w2 и X2 перехват — это (q-b)/w2. Теперь понятно, почему мы можем избавиться от q? Она является частью постоянной, и мы всегда можем смасштабировать b для достижения любой потери, поэтому будем считать, что Q=0, и в результате получим уравнение:
X2 = -X1*w1/w2 — b/w
Мы хотим найти веса W1 и W2 и смещение b так, чтобы они разделяли наши выходы или классифицировали их в особые разделы без перекрытия. Это ключ к линейной отделимости. Рис. 9.0 показывает число границ решений, которых будет достаточно, так что можно взять любые из них. Давайте возьмем простейшие:
W1=W2=1
b=-1
С этими значениями границей решения становится:
X2 = -X1*w1/w2 — b/w2 -> X2 = -1*X1 + 1
Наклон равен -1 и перехват X2 = 1. Если подключить входные векторы для логического AND в это уравнение и использовать активацию Fc(x), то мы получим верные выходные данные. Например, если X2+X1-1 > 0, то ответ нейроноды будет -1. Давайте попробуем с нашими входными данными для AND и посмотрим, что получится:
как видите, нейронные сети с соответствующим весом и смещением прекрасно решают задачу. Кроме того, есть целое семейство весов, которые будут делать это так же хорошо (раздвигая границы решения в перпендикулярном себе направлении). Однако есть важный момент. Без смещения или чувствительности будут возможны только прямые прохождения, т.к. перехват X2 должен быть 0. Это очень важно, и это основная причина использования чувствительности или смещения, так что этот пример был важен, поскольку из него ясно виден этот факт. Таким образом, ближе к делу — как найти нужные значения веса? Да, у нас теперь есть геометрические аналогии, и это начало нахождения алгоритма.
Обучение Хебба
Теперь мы готовы увидеть первый алгоритм обучения и его применение в нейронной сети. Один из самых простых алгоритмов обучения был изобретен Дональдом Хеббом, и он основан на использовании входных векторов для изменения веса так, чтобы вес создавал наилучшее линейное разделение входов и выходов. Увы, алгоритм работает всего лишь неплохо. Действительно, для ортогональных вводных это работает прекрасно, но для неортогональных алгоритм разваливается. Несмотря на то, что алгоритм не приводит к правильным весам для всех входов, он лежит в основе большинства алгоритмов обучения, поэтому мы начнем с него.
Прежде чем увидеть алгоритм, помните, что он лишь для одной нейроноды, однослойно нейронной сети. Можно, конечно, поместить много нейронод в слое, но все они будут работать параллельно и могут обучаться параллельно. Вместо использования одного вектора веса, мульти-нейроноды используют весовую матрицу. Во всяком случае, алгоритм прост, он выглядит примерно так:
- Входные данные в биполярной форме I=(-1,1,0,…-1,1) и содержат k элементов.
- Есть N входных векторов, и мы будем обращаться к их множеству как к J-элементу, напр. Ij.
- Выходы будут называться Yj, и есть K выходов, каждый для одного входа Ij.
- Веса W1-Wk содержатся в одном векторе W=(w1, w2,…wk)
Шаг 1. Инициализироавть все наши веса в 0, и пусть они содержатся в векторе W, состоящем из N записей. Также инициализировать смещение b в 0.
Шаг 2. От j=1 до n, делаем:
b = b + yj (Где y — желаемый результат
w = w + Ij * yj (Помним, что это векторная операция)
Конец.
Алгоритм — не более, чем «аккумулятор» сортов. Сдвиг границ решений основана на изменениях во вводе и выводе. Единственная проблема — то, что в некоторых случаях граница не будет двигаться достаточно быстро (и вообще не будет) и «обучение» не состоиться.
Так как же нам использовать обучение Хебба? Ответ на этот вопрос тот же, что и у предыдущей нейронной сети, за исключением того, что теперь у нас есть алгоритмический метод обучения сети, и эта сеть называется сетью Хебба, или Hebbian Net. В качестве примера давайте возьмем нашу верную логическую функцию и посмотрим, сможет ли алгоритм найти для неё надлежащие значения веса и смещения. Приведённое ниже суммирование эквивалентно запуску алгоритма:
w = [I1*y1] + [I2*y2] + [I3*y3] + [I4*y4] = [(-1, -1)*(-1)] + [(-1, 1)*(-1)] + [( 1, -1)*(-1)] + [(1, 1)*(1)] = (2,2)
b = y1 + y2 + y3 + y4 = (-1) + (-1) + (-1) + (1) = -2
Таким образом, W1=2, W2=2, и b=2. Это просто масштабированные версии значений W1=1, W2=2, B=-1, которые мы получили в предыдущем разделе. С помощью этого простого алгоритма мы можем обучить нейронную сеть (из одной нейроноды) ответить на массив вводных или классифицировать их как true/false, или 1/-1. А теперь, если бы у нас был массив таких нейронод, мы могли бы создать сеть, не просто определяющую вводные как да/нет, а и ассоциирующую вводные с некими паттернами. Это одна из основ для следующей структуры нейронных сетей, сетей Хопфилда.
Алгоритмы Хопфилда
Джон Хопфилд — это физик, которому нравится играть с нейронными сетями (что хорошо для нас). Он придумал простую (по крайней мере, сравнительно), но эффективную модель нейронной сети, названную Сеть Хопфилда. Она используется для ассоциирования, если вы ввели вектор x, то и на выходе получите x (я надеюсь). Сеть Хопфилда показана на рисунке 10.0. Это однослойная сеть с некоторым числом нейронод, равным числу входов Xi. Сеть полностью связана, и это означает, что каждая нейронода соединена с каждой другой нейронодой, а входы одновременно и выходы. Это может показаться вам странным, т.к. появляется обратная связь. Обратная связь является одной из ключевых особенностей сети Хопфилда, и она является одной из базовых основ для получения верного результата.
Сеть Хопфилда — это итерационная автоассоциативная память. Получение правильного результата может занять от одного до нескольких циклов. Позвольте пояснить: сеть Хопфилда получает ввод, а затем отдаёт его обратно, и результирующий вывод может быть и может не ыть желаемым вводом. Этот цикл обратной связи может пройти несколько раз до того, как будет возвращен входной вектор. Таким образом функциональная последовательность сети Хопфилда: сначала определить вес наших вводных, которые мы хотим ассоциировать, затем отдать входной вектор и посмотреть, что даст функция активации. Если результат такой же, как и наш оригинальный ввод, то всё получилось, если нет — возьмем результирующий вектор и скормим его сети. Теперь давайте посмотрим матрицу веса и алгоритм обучения, используемые в сетях Хопфилда.
Алгоритм обучения для сети Хопфилда основан на правиле Хебба и просто суммирует результат. Однако, поскольку сети Хопфилда имеют несколько входных нейронов, вес — уже не массив весов, а массив массивов, которые компактно содержатся в одной матрице. Таким образом весовая матрица W для сети Хопфилда создается на основе этого уравнения:
Дано:
- Вводные векторы в биполярной форме I = (-1,1,,…-1,1) и содержат k элеметнов.
- Есть N входных векторов, и мы будем обращаться к их множеству, как к j-элементу I, т.е. Ij.
- Выводы будут называться Yj, и есть k выходов, каждый для своего входа Ij.
- Весовая матрица W — квадратная, и имеет размерность kxk т.к. у нас есть k входов.
k
W (kxk) = е Iit x Ii
i = 1
Примечание: каждый внешний продукт будет иметь размерность К х К, так как мы умножаем вектор-столбец и вектор-строку.
И, Wii = 0 для всех i
Функция активации fh(x) показана ниже:
fh(x) = 1, if x і 0
0, if x < 0
fh(x) — функция шага с бинарным результатом. Это значит, что каждый ввод должен быть бинарным, но мы же уже говорили, что вводы биполярнны? Нууу да, это так, и это не так. Когда весовая матрица генерируется, мы конвертируем все входные векторы в биполярный формат, но при обычных операциях используем бинарную версию ввода и вывода, т.к. сеть Хопфилда также бинарна. Эта конверция не обязательна, но делает обсуждение сети немного проще. В любом случае, давайте рассмотрим пример. Скажем, мы хотим создать 4 ноды сети Хопфилда и мы хотим, чтобы они вызвали эти векторы:
I1=(0,0,1,0), I2=(1,0,0,0), I3=(0,1,0,1) Note: они ортогональны
Конвертируя в биполярные значени, получаем:
I1* = (-1,-1,1,-1) , I2* = (1,-1,-1,-1) , I3* = (-1,1,-1,1)
Теперь нам нужно вычислить W1,W2,W3, где Wi — продукт транспонирования каждого ввода с самим собой.
1 1 —1 1
1 1 —1 1
—1 —1 1 —1
1 1 —1 1W2 = [ I2*t x I2* ] = (1,-1,-1,-1)t x (1,-1,-1,-1) =
1 —1 —1 —1
—1 1 1 1
—1 1 1 1
—1 1 1 1
W3 = [ I3*t x I3* ] = (—1,1,-1,1)t x (—1,1,-1,1) =
1 —1 1 —1
—1 1 —1 1
1 —1 1 —1
—1 1 —1 1
Затем мы добавляем W1+W2+W3, в результате:
3 —1 —1 —1
—1 3 —1 3
—1 —1 3 —1
—1 3 —1 3
Обнуление главной диагонали дает нам окончательную матрицу веса:
0 —1 —1 —1
—1 0 —1 3
—1 —1 0 —1
—1 3 —1 0
Вооот теперь давайте потанцуем. Давайте введем наши оригинальные векторы и посмотрим на результаты. Чтобы сделать это, просто умнажаем вводы на матрицу и обрабатываем каждый вывод функцией Fh(x). Вот результаты:
I1 x W = (—1,-1,0,-1) and fh((—1,-1,0,-1)) = (0,0,1,0)
I2 x W = (0,-1,-1,-1) and fh((0,-1,-1,-1)) = (1,0,0,0)
I3 x W = (—2,3,-2,3) and fh((—2,3,-2,3)) = (0,1,0,1)
Вводы были отлично «вспомнены», как оно и должно бытьЮ, т.к. они ортогональны. В качестве последнего примера давайте предположим, что наш ввод (слух, зрение и т.д.) немного «шумноват» и содержит одну ошибку. Давайте возьмем I3=(0,1,0,1) и добавим немного шума, т.е. I3 noise = (0,1,1,1). Теперь посмотрим, что случится, если ввести этот «шумный» вектор в сеть Хопфилда:
I3 noise x W = (-3, 2, -2, 2) and Fh((-3,2,-2, 2)) = (0,1,0,1)
Удивительно, но исходный вектор «вспомнен». Это очень здорово. Таким образом у нас есть возможность создать «память», которая заполняется битовыми шаблонами, которые похожи на деревья (дуб, плакучая ива, ель и т.д.), и если мы введем другое дерево, например иву, которой не было в сети, наша сеть выведет (надеюсь) информацию о том, на что по её «мнению» ива похожа. Это одна из сильных сторон ассоциативных воспоминаний: мы не должны обучать сеть каждому возможному варианту ввода, нужно лишь столько, чтобы у сети возникали «ассоциации». Затем «близкие» вводы обычно сохраняются как изначально изученный ввод. Это основа распознавания изображений и голоса. Не спрашивайте меня, где я взял аналогию «дерева». Во всяком слуае, в конце нашей статьи я включил автоассоциативный симулятор сети Хопфилда, позволяющий создавать сети до 16 нейронод.
Мозг мёртв…
Вот и всё, что мы сегодня рассмотрим. Я надеялся добраться до сетей прецептрона, ну да ладно. Я надеюсь, вы хоть немного поняли, что такой нейронные сети и как создать рабочие программы для их моделирования. Мы рассмотрели основные термины и понятия, некоторые математические основы и некоторые самые распространенные модели сеетей. Однако, есть ещё множество вещей, которые можно узнать о нейронных сетях. Это перцептроны, нечеткая ассоциативная память или FAMs, двунаправленная ассоциативная память или BAMs, карты Кохонена, алгоритм обратного распространения сетей, адаптивной резонансной теории сети, и многое многое другое. Вот и всё, моя нейронная сеть зовет меня играть!
